介绍:

哈维尔[1955]——哈吉米[1962]算法能够用来判读一个度序列d是否是可图化的。

哈维尔[1955]——哈吉米[1962]定理:

 对于N > 1，长度为N的度序列d可以可图化当且仅当d*可以可图化

（d*是将d中最大的度delta删除，然后将当中delta个最大的度分别减去1得到的。

最小的可图化序列式d(1) = 0。）

证明:

充分性:

若N = 1。则是平庸的。对于N > 1。如果d为d(1) ≥ d(2) ≥ ...... ≥ d(n) 。

如果简单图G*拥有度序列d*，能够在G*中加入一个顶点V。

使得V与G*中度为d(2) - 1......d(delta+1) - 1的顶点邻接。

这些d(i)是d中的delta个最大度顶点，不一定是d*中的delta个最大度顶点。

必要性:

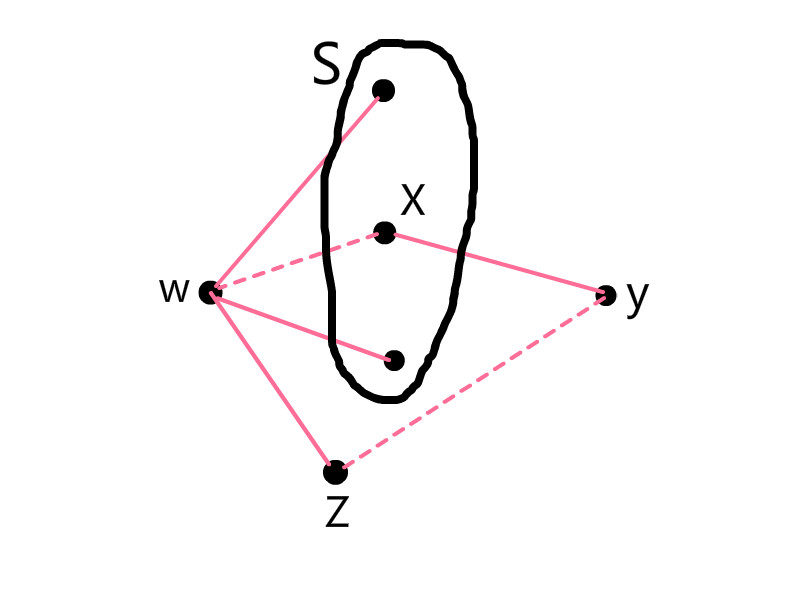
简单图G生成度序列d，然后G生成一个子图G*有度序列d*。让w为d中最大度delta的点。

S为delta个点的集合，当中有所期望的d(2)........d(delta + 1)。假设N(w) = S

则将w删除得到G*。

假设不然，则有些在S中的点与N(w)中的不同样，这时候。

能够通过在不改变每一个顶点的度的情况下。改变G的画法来添加| N(w) ∩ S |的个数。

因为| N(w) ∩ S |最多添加delta次。能够反复这一过程将G转化为G#

（拥有d且S中的点为w的邻接顶点）。

然后从G#中删除w得到拥有d*的G*。

因为N(w) ≠ S，能够选择点x属于S，点z∉s。且w与z有边，w与x无边。

我们希望通过在w与x之间加入边，删除w与z之间的边，但又不希望改变顶点的度。

因为d(x) ≥ d(z)而且w是z相连，则必定有一个点y与x邻接却不与z邻接。

这是採用一个2调换，加入边集{ wz, xy }，删除{ wx, yz }来添加| N(w) ∩ S |。

算法:

先将序列d逆序排序，得d(1) ≥ d(2) ≥ d(3) ≥ ........ ≥ d(n-1) ≥ d(n)。

delta = d1，将d1从d中删除。将d2一直到d（delta+1）的值都减去1得到新的度序列d*。

然后再将d*排序，循环。直到d*当中出现小于0的度，则不可能可图化，或者直到d*中全为0，则为可图化。

本质:

贪心算法

 

list1 = [ 4, 7, 7, 3, 3, 3, 2, 1 ]list2 = [ 5, 4, 3, 3, 2, 2, 2, 1, 1, 1 ]def havel_hakimi_algo( degree_list ):        degree_list.sort( reverse = True )    print degree_list    for degree in degree_list:        if degree < 0:            return False        if degree != 0:            remove_val = degree_list.pop( 0 )            for index in range( remove_val ):                degree_list[index] -= 1            havel_hakimi_algo( degree_list )    return Trueprint havel_hakimi_algo( list1 )print havel_hakimi_algo( list2 )